本期讨论基于dolfinx的Stokes方程的求解.

Strong Formulation

$$\begin{equation}\begin{cases}-\nabla\cdot T(u,p)=f & \text{in } \Omega \\\nabla\cdot u = 0 & \text{in } \Omega \\u = g & \text{on } \partial\Omega\end{cases} \notag\end{equation}$$

Define:  

$$D(u)=\frac12(\nabla u+(\nabla u)^T),$$

Then,

$$T(u,p)=2\nu D(u)-pI$$.

注意压力\(p\)只在梯度项出现，若\(p\)是解，则\(p+c\)也是解.

Weak Formulation

参考He Xiaoming: Finite Element Method.pdf

Find \(u\in H^1(\Omega) \times H^1(\Omega)\) and \(p\in L^2(\Omega)\), \(\forall v \in H^1_0(\Omega) \times H^1_0(\Omega),\ q\in L^2(\Omega)\) ：

$$\int_\Omega{2\nu D(u):D(v)}dxdy-\int_\Omega{p(\nabla\cdot v)}dxdy=\int_\Omega{fv}dxdy-\int_\Omega{(\nabla\cdot u)q}dxdy$$

把散度为0项乘-1直接加入方程右端

$$\begin{align*}a(u,v)&:=\int_\Omega{2\nu D(u):D(v)\mathrm{d}x\mathrm{d}y},\\b(u,q)&:=-\int_\Omega{\nabla\cdot u q}\mathrm{d}x\mathrm{d}y,\\(f,v)&:=\int_\Omega{f\cdot v}\mathrm{d}x\mathrm{d}y.\end{align*}$$

内积形式

$$\begin{align*}a(u,v) + b(v,p)&=(f,v),\\b(u,q)&=0.\end{align*}$$

容易写出离散的弱形式.

Example

$$\begin{equation}\begin{cases}u_1=20x^2(x-1)^2y(y-1)(2y-1)\\u_2=-20x(x-1)(2x-1)y^2(y-1)^2\\p=10(2x-1)(2y-1)\end{cases} \notag\end{equation}$$

\(f\)的表达式可以通过sympy自动推导.

Code

gitee repo: stokes-dolfinx: dolfinx框架实现Stokes方程FEM程序

Result

Convergence Rate

表格太长一行放不下

Figures

Velocity(\(128\times 128\))

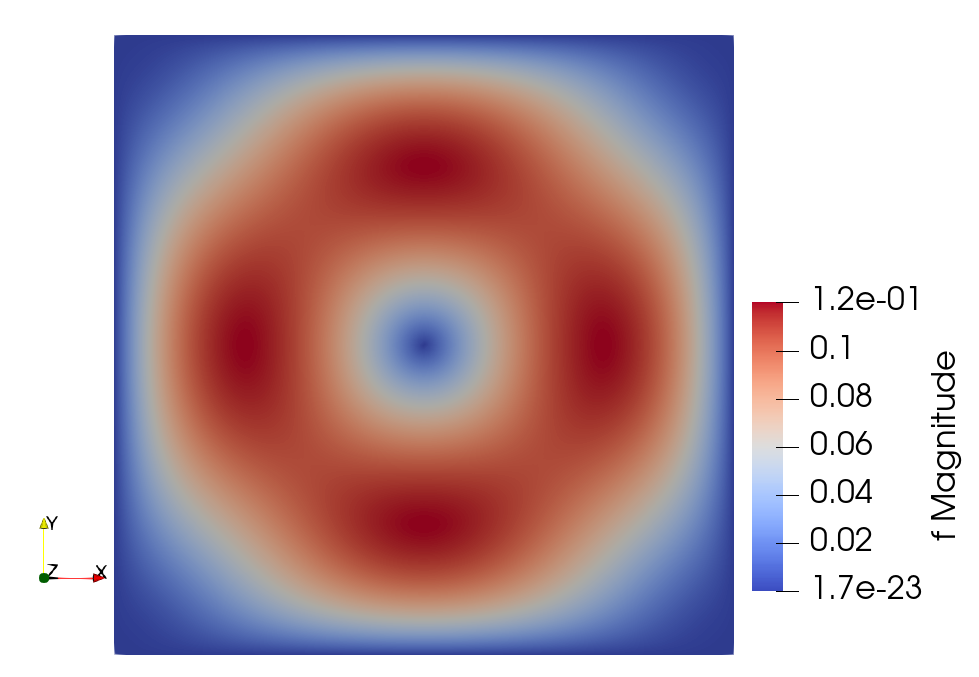
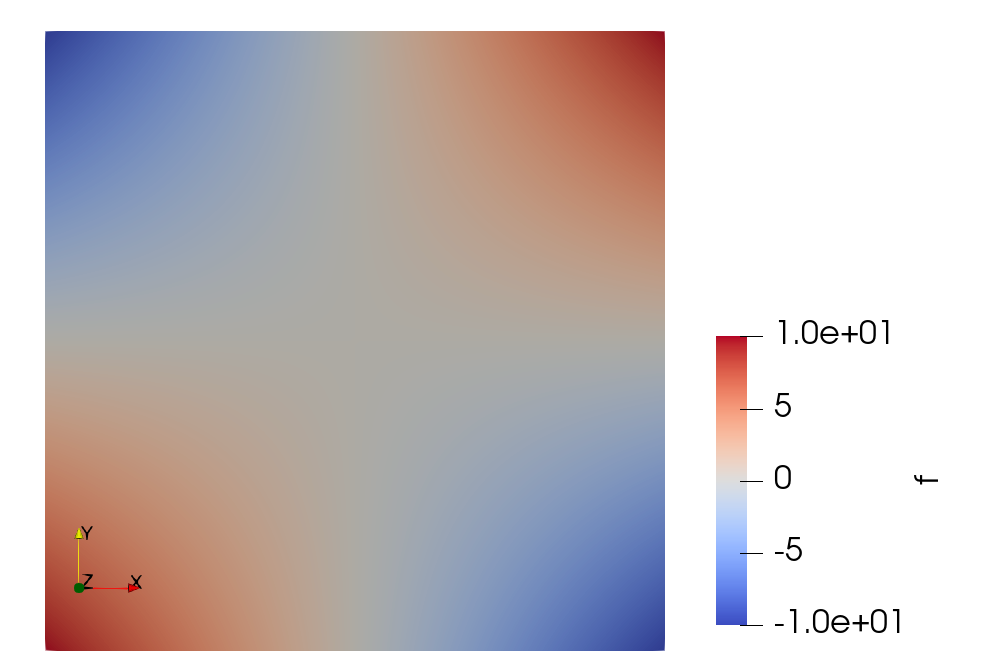
Pressure(\(128\times 128\))

Discussion

获取刚度矩阵和载荷向量的程序

def getStiffnessMatrix(A: PETSc.Mat):
    """
    获取刚度矩阵的值(np.array)
    """
    m, n = A.getSize()
    matrix_data = np.zeros((m, n))

    # 获取矩阵的所有非零元素
    row, col, val = A.getValuesCSR()

    # 将CSR格式的数据转换为密集矩阵
    for i in range(m):
        for j in range(row[i], row[i + 1]):
            matrix_data[i, col[j]] = val[j]

    return matrix_data

stiff_mat = getStiffnessMatrix(A=A)  # 刚度矩阵太大会oom(n=128)
load_vec = b.getArray()  # 载荷向量可以直接获取